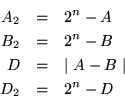Eksamen våren 1999 Datamaskinarkitektur
Les nøye gjennom oppgavene før du begynner og pass på å besvare alle spørsmålene. Alle hjelpemidler er tillatt. Deloppgavene vil bli vektlagt likt ved sensur, bortsett fra 5d) som vil få vekt 3.

Oppgave 1

a) Skriv 45 på binær, oktal og hexadesimal form. Vis fremagangsmåten.

b) Forenkle det boolske utrykket

\begin{eqnarray*}w\bar{x} + \bar{w} \bar{y} \bar{z} +\bar{w}\bar{x} z+ \bar{w} \bar{x} y\bar{z} \end{eqnarray*}


mest mulig ved hjelp av å bruke regneregler fra boolsk algebra.

c) Forenkle det boolske utrykket

\begin{eqnarray*}A\oplus B \oplus A \oplus \bar{B} \end{eqnarray*}


mest mulig.

d) Representer tallene A = 7 og B = 28 på 2'er komplement form med fortegn og utfør beregningen A - B og -A + B. Vis at svarene stemmer.

e) Ta utgangspunkt i at A og B er to positive n-bits tall og definer følgende størrelser:

\begin{eqnarray*}A_2 &=& 2^n - A \\ B_2 &=& 2^n- B \\ D &=& \mid A - B \mid \\ D_2 &=& 2^n- D \end{eqnarray*}


og representer tall med fortegn på 2'er komplement form:

\begin{eqnarray*}-A &=& 1A_2\\ +B &=& 0B \end{eqnarray*}


Vis at algoritmen for å legge sammen tall representert med fortegn på 2'er komplement form, virker for operasjonen -A + B.

Oppgave 2

a) Sett sammen to komplette adderere (full adder) til en kombinatorisk krets som legger sammen de to to-bits binære tallene A1A0 og B1B0 og leverer resultatet som tallet S2S1S0 gjennom tre output.

b) Du skal nå konstruere en krets som utfører den samme addisjonen, ved å designe den som en krets med 4 input A1,A0, B1, B0 og 3 output S2,S1,S0. Skriv ned sannhetstabellen for kretsen.

c) Bruk Karnaugh diagrammer til å finne forenklede uttrykk for output.

d) Anta at du tegner en to-nivå krets direkte fra de boolske uttrykkene i c). Hva er fordelen med denne kretsen i forhold til den du lagde i a) ?

Oppgave 3

a) En lås (latch) kan brukes til å lagre et bit. Forklar kort hvorfor en lås er uegnet som lagringselement i en sekvensiell krets og hvordan et egnet lagringselement kan konstrueres (ingen detaljer).

b) Hva er avbildet øverst i Fig. 1 ?

 
Figure: 3b)
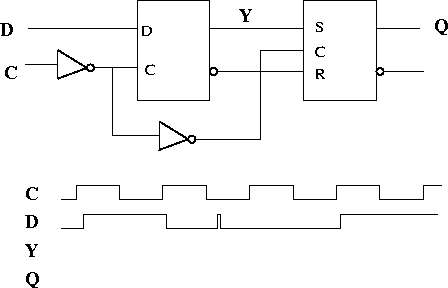\begin{figure} \begin{center} \mbox{\psfig{figure=D.ps,width=10cm} } \end{center} \end{figure}

Nedenfor er de logiske input-signalene C (klokka) og D plottet som funksjon av tiden. Tegn inn hvordan verdiene av Y og Q vil variere med tiden. Antyd hva 'spikeren' i D-signalet kan skyldes.

I resten av denne oppgaven skal du konstruere en sekvensiell krets som styrer en brusautomat og sørger for å gi brukeren en brus hver gang han har puttet på et riktig antall mynter. Brusen koster 15 kroner og automaten godtar bare fem og ti-kroninger. Brus-kretsen som du skal designe er knyttet til resten av automaten som vist i Fig. 2.
 
Figure: Brusautomat
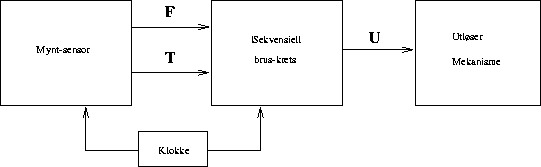\begin{figure} \begin{center} \mbox{\psfig{figure=brus.ps,width=12cm} } \end{center} \end{figure}

Eneste input er to logiske signaler, F og T, fra mynt-sensoren som er synkronisert med brus-kretsen. Hver gang sensoren har gjenkjent en femmer, setter den F til logisk 1 i en, og bare en, klokkesyklus. Når en tier blir gjenkjent, kommer en puls med T = 1. Ved alle andre tidspunkt er F og T null og de er aldri 1 samtidig. Hvis brukeren legger på en mynt som ikke er en tier eller femmer, kommer den bare ut av automaten igjen og myntsensoren sender ikke noe signal, bare null som vanlig.
Eneste output fra kretsen er U som skal være logisk 1 hver gang brukeren har lagt på mynter som tilsammen utgjør 15 kroner eller mer. Automaten skal ikke gi vekslepenger. Når 15 kroner er lagt på skal brus-kretsen altså sende et signal til utløsermekanismen og starte forfra igjen med å registrere myntinnkast (du trenger ikke å ta med mulighet for å initialisere/resette kretsen i ditt design).

c) Tegn et tilstandsdiagram for kretsen. Bruk færrest mulig tilstander.

d) Kretsen skal designes med D-vipper. Gi et binært nummer til hver tilstand og skriv ned tilstands-tabellen.

e) Bruk Karnaugh-diagram til å finne de boolske uttrykkene for vippe-inngangene og for output U. Bruk eventuelle ubrukte tilstander og input-kombinasjoner til å forenkle kretsen.

f) Tegn kretsen.

Oppgave 4

Vi skal i denne oppgaven se på en forenklet modell for en prosessor, en single-cycle datamaskin. Den skal ha en forenklet register fil med bare to 4-bits registere, R0 og R1. Datapath kan designes ved at register filen kobles til en ALU og RAM som vist i Fig. 3.
 
Figure: Datapath
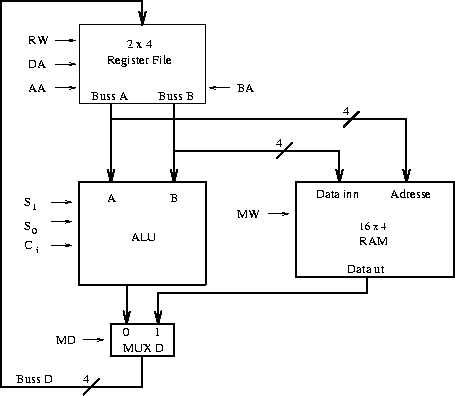\begin{figure} \begin{center} \mbox{\psfig{figure=machine.ps,width=10cm} } \end{center} \end{figure}

ALU'en består kun av en aritmetisk enhet med tre styrings-bit: S1, S0 og Ci. ALU'ens funksjonstabell er gitt ved

S0 S1 Ci Ut
0 0 0 A
0 0 1 A + 1
0 1 0 A+B
0 1 1 A+B+1
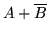1 0 0 $A+\overline{B}$
1 0 1 $A+\overline{B}+1$
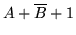1 1 0 A-1
1 1 1 A



Det er 9 bit som bestemmer hvilken operasjon datapath utfører og vi kan samle dem i et kontrollord: [DA, AA, BA, S1, S0, Ci, MD, RW, MW].
a) Skriv ned et kontrollord som får datapath til å legge sammen tallet i R0 med tallet i R1 og legge resultatet i R0.

b) Vi skal nå lage en hardwired kontrollenhet til datapath og skjematisk ser maskinen ut som i Fig. 4.
 
Figure: 4b)
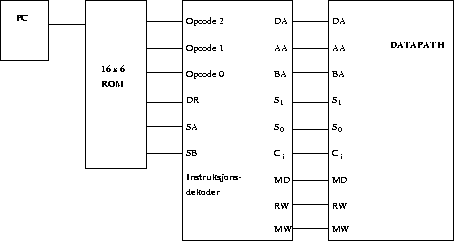\begin{figure} \begin{center} \mbox{\psfig{figure=single.ps,width=10cm} } \end{center} \end{figure}

Forklar kort (en til 2 setninger om hver) funksjonen til PC, ROM og instruksjonsdekoder.

c) En maskin-instruksjon er gitt av 6 bit på formen [Opcode 2, Opcode 1, Opcode 0, DR, SA, SB]. Instruksjonssettet for maskinen skal bestå av følgende seks instruksjoner:

Opcode Symbol Funksjon
000 ADD R[DR] $\leftarrow$ R[SA] + R [SB]
001 LD R[DR] $\leftarrow$ M[R[SA]]
010 ST M[R[SA]] $\leftarrow$ R[SB]
011 SUB R[DR] $\leftarrow$ R[SA] - R [SB]
100 INC R[DR] $\leftarrow$ R[SA] + 1
101 MOV R[DR] $\leftarrow$ R[SA]



Tegn en tabell som for hver av de seks instruksjonene viser hva S1, S0, Ci, MD, RW, MW er. Sett kryss, hvis verdien er vilkårlig.

d) Anta at vi i instruksjonsdekoderen kobler DR, SA og SB rett på DA, AA og BA. Finn S1, Ci og RW uttrykt ved de tre opcode-bitene og tegn den tilsvarende logikken i instruksjonsdekoderen (ikke beregn/tegn for de tre andre). Bruk de to ubrukte instruksjonene til å forenkle designet.

e) Anta at M[0] = 6 og M[1] = 4. Lag et symbolsk program som laster inn disse tallene fra minnet, utfør 4-6 og skriver resultatet tilbake til M[0]. Anta at tallene i R0 og R1 er ukjent når programmet starter.
(Programmet skal skrives med setninger hvor rekkefølgen på operandene er den samme som i maskin-instruksjonen. Setningen 'Sub R0,R1,R0' betyr dermed R0 $\leftarrow$ R1 - R0. Registere som ikke blir brukt er utelatt; I Instruksjonen 'LD R0,R1' blir f. eks. ikke SB brukt og den betyr R0 $\leftarrow$ M[R1] ).

f) Oversett programmet i e) til maskinkode og skriv ned linjene slik de må skrives i ROM.

g) Hvilke 4 bit ligger i M[0] etter at programmet har blitt kjørt ?
Skriv ned en setning i et høynivåspråk som ville gitt maskinkoden i delspørsmål f) som resultat etter kompilering.

Oppgave 5

a) Forklar en del av hva følgende assembler program utfører ved å gi en kort kommentar på hver av de 10 linjene mellom MerkeA: og MerkeB: (du skal altså ikke kommentere hele programmet).
.MODEL SMALL
.STACK 100h
.DATA
.CODE
   mov ax,@data
   mov ds,ax
   mov di,0
   mov cx,2
   mov ds:[di],cl
   hovedMerke:
      cmp cl,255
      je FerdigProg
      inc cl
      mov bx,0
      MerkeA:
         mov ah,0
         mov al,cl
         mov dl,ds:[bx]
         div dl
         cmp ah,0
         je hovedMerke
         cmp bx,di
         je MerkeB
         inc bx
         jmp MerkeA
      MerkeB:
         inc di
         mov ds:[di],cl
         jmp hovedMerke
   FerdigProg:
   mov  ah,4ch             
   int  21h      
END
b) Angi verdien av de tre første tallene i datasegmentet etter at programmet har kjørt.

c) Forklar kort hva programmet gjør og gi på grunnlag av det en matematisk karakteristikk av tallene som programmet legger i minnet.

d) Du skal i denne deloppgaven lage en assembler-prosedyre som utfører en liten animasjon i 320x200 modus; et grønt kvadrat som beveger seg over midten av skjermen fra venstre til høyre. Størrelsen på kvadratet skal være 40x40 og fargen grønn er 48 i paletten. Bakgrunnen er svart og denne fargen er gitt ved 0. Kvadratet skal gradvis komme til syne i venstre billedkant, bevege seg over skjermen og gradvis forsvinne i høyre billedkant. Skriv kun koden for prosedyren og ikke selve programmet. Du kan forvente at din prosedyre blir kalt fra en hovedprosedyre som har initsialisert es til å peke på videosegmentet, har switchet til 320x200 modus og deretter kaller din prosedyre en eller flere ganger. For at animasjonen i praksis skal bli synlig på skjermen, må man legge inn en venteløkke, men det trenger du ikke ta hensyn til her. Du kan velge om du vil følge den skisserte metoden nedenfor eller lage din egen metode.
Lag først en prosedyre tegnLinje som tegner en vertikal linje med lengde 40 midt på skjermen i en avstand fra venstre bildekant som prosedyren forventer er gitt ved bx. Den forventer også at fargen er gitt av al. Skriv deretter en prosedyre som ved gjentatte kall til tegnLinje (etter å ha satt verdiene på al og bx), lager animasjonen av kvadratet som beveger seg over skjermen.

-SLUTT-

About this document ...

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -show_section_numbers -split 0 -no_navigation exV99.

The translation was initiated by Haarek Haugerud on 2000-05-09

Haarek Haugerud
2000-05-09