


Next: About this document ...
Første obligatoriske oppgave
Datamakinarkitektur våren 1999
Innleveringsfrist: Fredag 5. Mars.
Denne oppgaven skal leveres individuelt fra hver student.
Oppgave 1
La w,x,y og z betegne booleske variable.
a) Vis algebraisk at
b) Forenkle følgende uttrykk mest mulig:
c) Bruk Karnaugh-diagram til å forenkle den booelske funksjonen
Skriv funksjonen også som et produkt av summer på enklest mulig form.
Oppgave 2
Du skal i denne oppgaven konstruere en digital krets som sammenlikner
størrelsen av to to-bits binære tall
X = x1 x0 og
Y = y1 y0.
Kretsen skal ha to utganger l og g hvor l = 1 hvis X < Y og l = 0 hvis
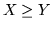 ,
og hvor g = 1 hvis X > Y og g = 0 hvis
,
og hvor g = 1 hvis X > Y og g = 0 hvis 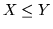 .
.
a) Forklar hvorfor X = Y hvis og bare hvis g = l = 0.
b) Lag en sannhetstabell for kretsen.
c) Sett opp forenklede booleske funksjoner for kretsen.
d) Tegn kretsdiagram. Bruk kun NAND og NOT porter.
e) Anta at du får inn bare ukomplementerte input verdier
x1, x0, y1, y0.
Tegn et nytt kretsdiagram med NOT porter og med AND og OR porter
som kun har to innganger.Du skal lage kretsen med færrest mulig
porter og den skal maksimalt ha 4 NOT porter og 10 AND/OR porter.
Prøv om du klarer å lage hele kretsen med bare
3 NOT porter og 8 AND/OR porter (eller om mulig med enda færre).
Oppgave 3
Konstruer en XOR-port ved hjelp av en 1-til-2 linjers dekoder, en 2x1 multiplekser og
en NOT-port.
Oppgave 4
Representer tallene +45 og -14 på 2'er komplement form med fortegn og legg dem sammen.
Sjekk at svaret er riktig. Gjør det samme for -45 og +14.



Next: About this document ...
Haarek Haugerud
1999-02-19