Oppgaver til onsdag 7. mars 10.30 - 11.10
Oppgaver til labtimene
A4 Lag en komplett adderer (Full Adder", FA) makro. Form makroens template slik at den lett kan inngå i makroen du skal lage i neste punkt. Den skal virke som angitt i følgende sannhetstabell:
| X | Y | Z | S | C |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Lag en testkrets med interactive input's og LED's og kontrolle at makroen virker som den skal.
A5 Bruk 4 av FA-makroen fra punkt A4 til å lage en 4-bit
aritmetisk krets. Denne skal vi senere bruke som vår datamaskins
ALU. Lag en ALU makro av denne. Kretsen skal både kunne subtrahere
og addere. Det skal antas at tall blir representert på 2'er-komplement
form med fortegn (addisjon vil da selvsagt virke utmerket også om
man bruker kun positive tall). ALU-makroen skal ha 2x4 input med 4-bits
tallene A og B som skal behandles, og 4 output som gir resultatet, et 4-bits
talll D. I tillegg skal ALU-makroen ha 3 kontroll input, S1, S0 og Ci som
skal brukes til å styre ALU'ens funksjon. Disse kontroll input skal
styre ALU'en etter følgende tabell:
| S1 | S0 | Ci = 0 | Ci = 1 |
| 0 | 0 | D = A (overfører A til D) | D = A + 1 (inkrement) |
| 0 | 1 | D = A + B (addisjon) | D = A + B + 1 |
| 1 | 0 | D = A + ikkeB | D = A + ikkeB + 1 (subtraksjon) |
| 1 | 1 | D = A - 1 (dekrement) | D = A (overfører A til D) |
Dermed kan de ønskede funksjoner senere oppnås ved å
velge riktige input til S1, S0 og Ci. Kretsen kan designes ved å
først lage en 4-bits mentebølgeadderer og la Ci være
carry-input til denne addereren. Deretter sendes tallet A rett inn i addereren,
mens det andre 4-bits tallet som sendes inn i addereren er henholdsvis,
0, B, ikke B og 1 for de fire radene i tabellen over. Dette oppnås
ved å koble bitene til B-tallet til litt ekstra logikk, så
de ønskede verdiene går inn i addereren. En mulighet er å
bruke den kvadruple 4x1 MUX'en fra deloppgave A3, koble 0, B, ikke
B og 1 til MUX'en og la S1 og S0 velge hva som sendes videre inn i addereren.
Det er også mulig å oppnå det samme med færre porter
om man setter opp et lite K-diagram for den ønskede logikken.
Endelig skal makroen ha to kontroll-output, Co og V. Co er carry fra den siste av FA'ene og V er et bit som er 1 om det har forekommet overflow i beregningene, slik som vist i FIGURE 3-32 i læreboka.
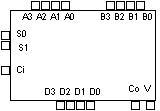
Makro template for ALU'en kan f. eks. se ut som på figuren. Lag
en testkrets med interactive input's og LED's og kontroller at den virker
som den skal.