Subsections

3 Forelesning 29/1-24(2 timer). Vipper og registre, CPU-arkitektur 


Avsnitt fra Tanenbaum: 1.3.1
Slides brukt i forelesningen

3.1 Forelesningsvideoer

Uredigert opptak av første del av forelesningen ( 00:45:07)
Uredigert opptak av andre del av forelesningen ( 00:59:02)

Opptak av forelesningen inndelt etter temaer:

os3del1.mp4 (06:26) Innledning om forelesninger, oblig1 og os-grupper i Canvas
os3del2.mp4 (02:28) Om dagens forelesning
os3del3.mp4 (05:49) Slides: Sist, Adderings-krets, numerisk overflow
os3del4.mp4 (05:45) Slides: Arithmetic Logic Unit (ALU), ALU-operasjoner og tidlig ALU-design
os3del5.mp4 (03:28) Slides: Vipper og registere
os3del6.mp4 (01:19) Slides: Første forsøk på å lagre en bit
os3del7.mp4 (03:17) Slides: Andre forsøk på å lagre en bit
os3del8.mp4 (05:26) Slides: Tredje forsøk, D-latch
os3del9.mp4 (01:21) Slides: Spørsmål: hva var problemet med de to første løsningene?
os3del10.mp4 (07:50) Slides: Shift-register av D-latch'er. Menneskelige-D-latcher. Løsning: D-vippe med klokke
os3del11.mp4 (01:15) Gjennomgang av svaret for første poll om port-diagram.
os3del12.mp4 (01:32) Gjennomgang av svaret for andre poll om port-diagram.
os3del13.mp4 (06:11) Slides: Sammenslåing av to D-latcher til en D-vippe
os3del14.mp4 (01:53) Slides: Tellere
os3del15.mp4 (04:34) Slides: Von Neumann arkitektur
os3del16.mp4 (04:05) Slides: Beregningsenheter
os3del17.mp4 (05:07) Slides: Simulering av CPU, Datapath
os3del18.mp4 (03:28) Slides: Høynivåkode og maskininstruksjoner
os3del19.mp4 (06:24) Slides: Assemblykode og maskinkode for simulerings-CPU'en
os3del20.mp4 (01:49) Slides: Branch control
os3del21.mp4 (05:09) Demo: Hvordan kjøre og programmere simulerings-CPU'en med maskinkode

3.2 Sist

I forrige forelesning så vi på hvordan man med datamaskinarkitekturens atomer, transistorer, kan lage logiske porter. Videre så vi på hvordan enhver logisk enhet kan defineres utifra en sannhetstabell som gitt hvilke logiske signaler som kommer inn i enhet sier hva som skal komme ut. Utifra en slik sannhetstabell kan man skrive ned et uttrykk ved hjelp av binær logikk og forenkle dette utrykket med boolsk algebra og andre metoder. Man ender da opp med et uttrykk beskrevet med de logiske operatorene AND, OR og NOT. Til slutt kan man konstruere en logisk krets utifra det logiske uttrykket og utifra dette kan man lage en fysisk enhet som nøyaktig oppfyller den sannhetstabellen man satt opp. Dette kan gjøres på en kretskortfabrikk hvor hver eneste transistor legges inn på kretskortet på samme måte som i den logiske kretsen. Dermed kan man lage hvilke som helst type logiske enheter. Ved å fysisk koble sammen slike enheter med ledninger, kan man lage komplekse kretser som for eksempel legger sammen to 64-bits tall. Men etter å ha lagt sammen to tall trenger vi å kunne lagre dette resultatet og umiddelbart etterpå for å kunne bruke resultatet i nye beregninger. For å kunne lage en datamaskin trenger vi derfor lagerenheter.

3.3 ALU

Vi har vist at ved å sette sammen flere bokser som adderer enkelt-siffer med mente, kan man lage en adderer som ser omtrent ut som i Fig. 24.

Figure: C = A + B (12 = 6 +6). Logiske kretser med AND, OR og NOT er konstruert inne i boksen på en slik måte at de alltid regner ut riktig resultat. Kretsen leser fra og skriver til 4-bits registre.

\includegraphics[width=7cm]{fig/adder.pdf}

En slik løsning kan systematisk utvikles til å legge sammen 32 og 64 bits tall. Når det gjelder addisjon, gjøres det noen forbedringer på metoden vi brukte for at det ikke skal ta for lang tid for mente å bevege seg fra siste til første siffer. Men det vil bruke mye plass om man må ha en slik enhet for enhver matematisk eller logisk operasjon som man ønsker å utføre. Det viser seg at man kan konstruere en krets som ved hjelp av små endringer både kan addere, subtrahere, øke med en, sammenligne, gange med 2, og så videre. Man styrer hvilken av disse operasjonene enheten skal utføre ved hjelp av kontroll-bits. I Fig. 25 ser vi en tilsvarende krets med to ekstra kontroll-bit.

Figure: En ALU med fire funksjoner. C = A + 1 (7 = 6 + 1). Her styrer kontroll-bitene S0 og S1 kretsen til å øke A med en og legge resultatet i C. Dette kan for eksempel skje ved S0 = 0 og S1 = 0, mens ved S0 = 0 og S1 = 1 ville ALU-en legge sammen tallene.

\includegraphics[width=7cm]{fig/alu.pdf}

Dette gjør det mulig å kode inn flere lignende operasjoner inn i kretsen, og den blir til en liten ALU (Arithmetic Logic Unit). Eksakt hvilken funksjon som utføres bestemmes av kontroll-bitene. En ALU er selve hjernen i en CPU hvor alle beregninger blir gjort. I tillegg inneholder CPU registre (4-bits registre i figuren) for å lagre data og en kontrollenhet som oversetter maskininstruksjoner til styringsbit for registre og ALU slik at riktig instruksjon blir utført. Konseptet ALU ble innført av matematikeren John von Neumann i forbindelse med konstruksjonen av en av verdens første datamaskiner, EDVAC i 1945. Det følgende er operasjoner som alle ALU-er kan utføre:

Figure: ALU-en til EDSAC 2 fra 1958 hadde radiorør, som senere ble erstattet av transistorer.
Image edsac2-arithmetic-logic-unit
Neste steg er å forstå hvordan man kan bruke AND, OR og NOT-porter til å lage registre som kan lagre data inne i CPUen.

3.4 Lagring av data: vipper og registre

Man kan lagre og representere nuller og enere ved å bruke små kondensatorer som lagrer elektrisk ladning. Men dette er ikke like raskt som om man bruker logiske porter lagd av transistorer. I tillegg må kondensator-lagerenheten jevnlig oppfriskes, typisk 10 ganger i sekundet. Men det er denne teknologien som brukes i RAM og dette skal vi se på senere. Hovedproblemet er at denne teknologien gjøer RAM tregere. For å lage en lagerplass som hurtig kan leses å endres må vi bruke logiske porter. Av slike porter kan man lage en lagerenhet som kan lagre nuller og enere og disse kalles vipper(engelsk: flip-flops). Dette er den siste byggestenen vi trenger for å kunne lagre dataene i beregningene som kretsene gjør. Det er mulig å lage en slik lagerenhet ved hjelp av porter. Denne vil da bli ekstremt hurtig, like hurtig som resten av CPU-en og langt hurtigere en lagringsenhetene i RAM. En vippe er den grunnleggende lagringsenheten i CPU-en og brukes til all lagring av data internt, inkludert cache (mellomlagring) i CPU-en og cache mellom CPU og RAM. I de neste avsnittene skal vi se på hvordan en slik lagringsenhet kan konstrueres. Først lager vi en enhet som kan lagre en bit, slike kan settes sammen til store registre med 32 og 64 bit.

3.4.1 Lagringsenhet for en bit, D-lås(D-latch)

For å lagre noe med porter, må vi lage en lukket krets slik at bit-verdiene bevares. Et første forsøk er vist i Fig. 27.

Figure: Lagring av verdien Q = 1

\includegraphics[width=6cm]{fig/dlatch1.pdf}

Men et opplagt problem med denne lagringen er at verdien ikke kan endres. Ved å legge inn en OR-port foran NOT-porten 2 får man en mulighet til å legge inn en verdi D, som vist i Fig. 28.

Figure: Endring av verdien Q til 0
\includegraphics[width=10cm]{fig/dlatch2.pdf}

For denne lagringsenheten kan man endre verdien. Hvis man sender inn D=0 som på figuren vil den etterfølgende NOT-porten sende en ener inn i den øverste OR-porten. Hvis det kommer en ener inn i en av inngangene til en OR-port vil det alltid gå en ener ut, og dermed vil kretsen lagre 0 etter at eneren har gått igjennom den siste øverste NOT-porten. Hvis vi prøver å lagre D=1, kan man se at den nederste OR-porten alltid vil gi en ener ut. Dermed sendes en null opp til den øverste OR-porten som sammen med en null fra NOT-porten rett etter D gir en null og dermed en ener ved Q3.

Dermed kan vi legge inn verdire i lagringsenheten, men problemet nå er at vi alltid vil legge inn det som kommer inn i D. Noen ganger ønsker vi å bevare det vi har lagret til senere og for å få til den muligheten legger vi inn et kontroll signal C som er slik at

Det kan gjøres som vist i Fig. 29.
Figure: D-lås(latch). D står for data. Dette er en lagringskrets som kan skru lagring av og på. Den nederste boksen symboliserer hele kretsen.
\includegraphics[width=12cm]{fig/dlatch3.pdf}

Hvis C = 1 så vil kretsen fungere nøyaktig som kretsen over i Fig. 28, fordi en ener inn i en AND-port alltid vil gi verdien til den andre inngangen ut og dermed er alt nøyaktig som i kretsen over. Hvis C = 0 vil kretsen fungere nøyaktig som den første kretsen i Fig. 27. Dette er fordi en null inn i en AND-port alltid gir 0 ut, og dermed kommer det en null inn i begge OR-portene. Men en null inn i en OR-port gir alltid verdien til den andre inngangen og dermed fungerer kretsen som den aller første og enkleste, kretsen beholder bare den verdien den har lagret.

3.4.2 Simulering av shift-register med studenter

Et problem med å bruke en D-lås til å lagre data i en CPU er at man trenger kontroll på når data lagres av en D-lås og når data leses av neste D-lås. Om data i tillegg går igjennom kretser som endrer data blir problemet større, for da vil det være ulik tid som går med til å fullføre beregninger av ulik type. For eksempel tar en multiplikasjon av to tall lenger tid enn en addisjon. Under forelesningen skulle hver av de åtte deltagerne fungere som en D-lås. Det vil si, de skulle kun se på D-låsen foran seg og endre sin verdi til dens verdi når input fra C er 1. Når foreleser løftet hånden, betydde det C = 1 og at alle D-låser skulle virke ved å endre sin verdi til den samme verdien som nærmeste D-lås hadde. På samme måte som i Fig. 32 der hver av D-låsene hele tiden leser av verdien Q til den D-låsen som står til venstre for seg og dette blir til input D for den selv. Når C = 1 vil den derfor endre sin Q-verdi til samme Q-verdi som D-låsen til venstre for seg. På samme måte stilte åtte studenter, dobbelt så mange som i figuren, opp etterhverandre som vist i Fig. 31.

Figure: Åtte menneskelige D-låser på rad. Armen opp betyr 1, ned betyr 0. Hver D-lås leser verdien til D-låsen til høyre for seg (motsatt retning som for D-låsene i i Fig. 32).
\includegraphics[width=12cm]{fig/vippe1.pdf}

Når foreleser hever armen og alle begynner å virke, er problemet at det kan være litt ulikheter mellom hvor fort de menneskelige D-låsene reagerer på endringer til D-låsen foran dem. Dermed kan for eksempel en endring fra figuren over bli til resultatet i Fig. [*], at en ekstra verdi 1 dukker opp. Det kan skje hvis den kvinnelige vippen nummer 4 fra venstre leser av sin verdi raskere enn kvinnelig vippe nr 6. Og mannlig vippe nr 5 i mellom dem er raskere enn mannlig vippe nr 7. En slik måte å propagere data på vil være ustabil i forhold til selv svært små forskjeller i tidsbruk og vil også være helt ubrukelig som metode i en CPU.

Figure: De menneskelige D-låsene reagerer ikke nøyaktig like fort og dermed kan dette bli neste tilstand for arrayet av bits, der en ener for mye har dukket opp.
\includegraphics[width=12cm]{fig/vippe2.pdf}

For å kunne kontrollere nøyaktig når dataene blir overført og gjøre overføringen uavhengig av små svingninger i tempo på de involverte kretsene, innfører man en klokke som med jevne av og på singnaler styrer dette. I forelesningen ble dette gjort ved at foreleser svinger armen opp og ned i et jevnt tempo med en frekvens på omtrent en halv Hertz, altså hvert andre sekund. Når dette gjøres og alle studentene virker som de skal, kan man se at de to bit'ene beveger seg bortover uten at noe informasjon blir borte. Svingningene opp og ned med armen tilsvarer den berømte CPU-klokken, som typisk svinger med en frekvens på 2-4 GHz, noe som betyr flere milliarder svingninger av og på i løpet av et sekund.

3.4.3 Vipper(flip flops)

Nå er vi nesten fremme; vi har sett hvordan en krets kan gjøre operasjoner som å legge sammen to tall og vi har nå en lagringsenhet som input kan tas fra og resultatet lagres i. Men det er et problem som gjenstår. Hvis vi bare kobler sammen disse enhetene, har man ikke kontroll på den logiske flyten av data. Selvom signalene går med nesten lysets hastighet, tar det litt tid fra signalene kommer inn på den ene siden av en regnekrets til det rette svaret kommer ut i den andre enden. Et eksempel på hvordan flyten blir ukontrollert får man om man kobler sammen fire D-låser i hensikt å lage et shift-register som vist i Fig. 32.
Figure: D-latch(lås). Fire D-låser settes sammen til et shift-register.
\includegraphics[width=11cm]{fig/dlatches.pdf}
Vi ønsker å kunne utføre en operasjon som 1010 -> 0101 som med binære tall er det samme som å dele på 2. Men om vi sender en 1'er inn i C (som betyr at D-låsen skal lese inn en ny verdi) som i figuren, har vi ikke kontroll på hvor lang tid det tar for den nye verdien å bli lest, og med en gang den blir lest, vil neste D-lås lese den nye verdien og så videre4. Dermed har man ikke kontroll på hvor langt informasjonen går før man eventuelt skal sende inn en 0'er inn i C for å stoppe innlesningen og lagre resultatet. I mer kompliserte kretser vil det også være et problem at det kan variere mye hvor lang tid det tar før beregningen er ferdig og neste bit klar for lesing. Dette problemet løser man i en CPU ved å sette sammen D-låser to og to og å ha en klokke som sender et av og på signal med en viss frekvens, for eksempel 1 GHz, eller en milliard endringer mellom null og en i sekundet. Hvordan dette kan gjøres er vist i Fig. 33.
Figure: To master og slave D-låser blir til en D-vippe. Klokken går av og på og styrer når de endelige dataene lagres av slaven. Dette er selve CPU-klokken, som typisk har en frekvens på 1-3 GHz.
\includegraphics[width=12cm]{fig/dvippe.pdf}
Når klokken sender en 1'er, vil en slave lese inn og lagre det som master lagret når klokken rett før sendte en 0. Dermed vil data kunne bevege seg fra D-vippe til D-vippe på en kontrollert måte. Det er slaven som holder den gjeldene verdien for vippen som den leser fra master i starten av en klokkesyklus. Dette er verdien til bit'en i denne klokkesyklusen. Et shift til høyre vil forflytte alle slave-verdiene synkronisert, slik at de flytter seg hver gang klokken går over fra å sende 0 til å sende 1. Til en viss grad kunne man se at det fungerte under student-simuleringen.

Oppsummert vil tiden deles inn i små klokke-tikk og innenfor et slikt tikk må

CPU-klokken er helt essensiell for å synkronisere dataene, for hvert tikk av klokken kan et nytt sett av beregninger gjøres, for eksempel å utføre en maskin-instruksjon.

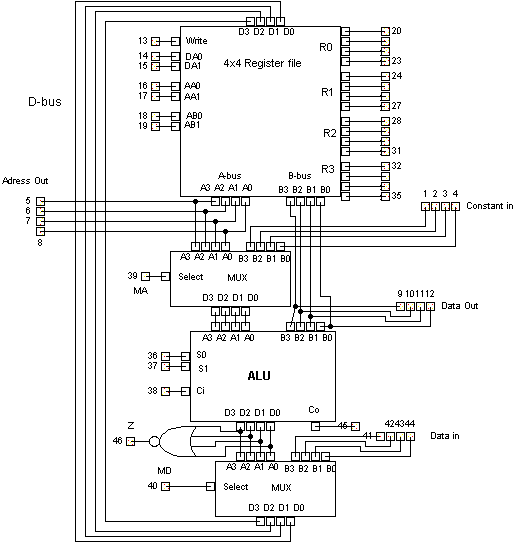
Data lagres i CPU-en med slike vipper og slike samlinger av vipper som vi lar representere tall kalles registre. En 32bits CPU har registre som består av 32 vipper og dermed kan lagre 32bits tall. En 64bits CPU har 64bits registre. Vi skal nå se på en simulering av en virkelig CPU laget med verktøyet Digital Works. Denne CPU-en er svært liten, det er en 4bits CPU og den har altså 4bits registre. Men bortsett fra størrelsen, kan den i prinsippet gjøre alle beregninger som en moderne CPU kan gjøre og den virker på helt samme måte. Grunnen til at en moderne CPU er mye mer komplisert er i tillegg til at de er større, er at arkitekturen er endret for at beregningene skal gå rasker. Registrene sitter i begge ender av beregningene. Hvis to tall skal legges sammen, kobles output for to registre til ALU-en som inneholder addisjons-logikken. Utgangen av ALU kobles så til registeret som skal lagre resultatet. I denne simulerte maskinen gjøres en ny operasjon eller instruksjon hvert klokke-tikk.

3.5 Tellere

For å kunne løpe gjennom instruksjoner i et program, trenger man en teller som kan telle oppover for hvert klokke-tikk. Et program som kjøres av en CPU består av en rekke instruksjoner som skal gjøres etterhverandre. Den starter med instruksjon nummer en som ligger i RAM og så teller den seg oppover til instruksjon nummer 2 og så videre ved hjelp av telleren. Noen ganger er det behov for å hoppe i koden, som ved en If-test, og da settes telleren til det instruksjonsnummeret det skal hoppes til og teller videre derfra. I Fig. 34 ser vi en 2-bits teller som kan telle fra 0 til 3. Ved å la verdien disse vippene har, D-vipper i dette tilfellet, representere hvert sitt siffer i et binært tall, kan de tilsammen representere tallene 0-3. For å lage større tall, trenger vi bare flere vipper.

Figure: En 2-bits teller
Image 2bitTeller

3.6 CPU-arkitektur

Den vanligste datamaskinarkitekturen som brukes, i hvertfall i hovedtrekk, av de fleste av dagens datamaskiner, er von Neumann-arkitekturen. Den ble definert i rapporten "First Draft of a Report on the EDVAC" av matematikk-professoren John von Neumann i 1945. Fig. 35 viser en skisse av denne arkitekturen.
Figure: Von Neumann arkitektur
Image vonNeumann
De viktigste delene av von Neumann arkitekturen er CPU(Central Processing Unit) inneholder kontrollenheten, ALU og registre (de to siste utgjør tilsammen datapath). Et problem med denne arkitekturen blir omtalt som 'the Von Neumann bottlenck'. Det kommer av at instruksjoner og data deler samme data-buss. I Hardvard arkitekturen er strømmen av instruksjoner og data inn til CPU fysisk adskilt. I de fleste moderne løsninger er en Modified Harvard architecture tatt i bruk som løser flaskehalsen ved å ha forskjellige cache-kanaler for instruksjoner og data.

3.7 Beregningsenheter

Følgende er noen typer beregningsenheter med økende grad av kapasitet. En CPU er meget anvendelig ved at den er så generell at den kan programmeres til å gjøre alle mulige beregninger. De etterfølgende enhetene er i økende grad spesialiserte og dermed raskere til å utføre de spesielle beregningene de er lagd for å gjøre.

3.8 En simulering av en datamaskin

Fig. 36 viser arkitekturen til en komplett CPU som kan utføre programmer skrevet i såkalt maskinkode. Det er gjort visse endringer i forhold til von Neumann arkitekturen, den vesentligste er at maskininstruksjonene er lagret i en ROM (Read Only Memory) inne i CPUen. Vanligvis hentes de fra RAM fortløpende og lagres i instruksjonsregisteret i CPU-en før de kjøres.

I en reell CPU består portene av fysiske halvledere og ledningene av fysiske elektriske ledninger brent inn i kretskort i ekstremt liten skala. Alt denne maskinen forstår er nuller og enere og for å gi den beskjed om hva den skal gjøre, må disse beskjedene gis i form av en binær kode. I denne maskinen består instruksjonene av 8 bit og for eksempel betyr maskininstruksjonen 01001011 at den skal legge sammen tallet som er lagret i register R2 og tallet som er lagret i register R3 og lagre resultatet i R2. Instruksjonen er delt opp slik at de 4 første bit'ene 0100 betyr ADD og at operasjonen 'legg sammen' skal utføres. De to neste bitene 10 betyr R2 og de to siste 11 betyr R3. Det eneste CPU-en gjør er å utføre denne type instruksjoner om og om igjen.

Figure: En komplett CPU tilkoblet RAM
Image machine

En samling slike instruksjoner utgjør et program og i denne maskinen er de lagret i boksen merket ROM. Vanligvis ligger maskinkoden som skal utføres sammen med programmets data i RAM, boksen nede i høyre hjørnet. I denne datamaskinarkitekturen ligger bare programmets data i RAM og det finnes instruksjoner som flytter data mellom RAM og registrene, men vi skal i første omgang ikke bruke dem her. Kanalene som går mellom datapath og RAM er data-bussen. I en von Neuman-arkitektur sendes både data og instruksjoner over denne bussen. Men i vårt tilfelle ligger ikke instruksjonene i RAM men i en spesiallaget ROM, dette er ikke så vanlig i CPU-arkitekturer. Men totalt sett minner denne arkitekturen derfor mer om Harvard-arkitekturen hvor instruksjoner og data sendes inn til CPU-en på to forskjellige busser. Det finnes typisk noen hundre registre i en standard CPU, men disse blir bare brukt til mellomlager, mer permanente verdier som variabler i et program, lagres i RAM som har mye større kapasitet. Enda større datamengder som man ønsker å lagre når maskinen skrus av, lagres på disk.

Figure: Datapath med fire 4-bits registre og ALU. En ofte brukt operasjon består i at data føres inn i ALU fra registrene via A og B og at resultatet etter beregningen lagres i et register.
Image datapath

Men hvor er selve hjernen til CPU-en som kan legge sammen tall, trekke dem fra hverandre, sammeligne dem og så videre? Den sitter inne i Datapath der inngangen til to valgte registre kan kobles til ALU-en (Arithmetic Logic Unit). Og inne i denne skjer selve operasjonen. Verdien på input-ledningene S0 og S1 avgjør hvilke operasjoner som utføres, ADD, SUB, SHIFT, etc. Andre input-ledninger avgjør hvilke registre som ledes inn i ALU og i hvilket register resultatet lagres. Disse input'ene kommer fra instruksjonsdekoderen som for hver instruksjon trykker på de rette knappene for å få den utført. For eksempel sørger instruksjonsdekoderen for at maskininstruksjonen 01001011 nevnt ovenfor virkelig fører til at ALU legger sammen tallet som er lagret i register R2 med tallet som er lagret i register R3 og lagrer resultatet i R2.

3.9 Fra høynivåkode til CPU-beregning

Så godt som all programvare blir skrevet i et høynivåspråk som Java eller C. Dette er språk som vanlige CPU-er ikke forstår og høynivåkode må derfor oversettes til maskinkode for at den skal kunne utføres. Oppgaven med å oversette fra høynivåkode til maskinkode utføres vanligvis av et program, en kompilator. Vi skal se på et enkelt eksempel og vise hvordan en liten bit høynivåkode kan oversettes til et kjørbart program i vår virtuelle Digital Works prosessor. Vi starter med følgende kodesnutt: 

S = 0;
for(i=1;i < 4;i++)
{
   S = S + i;
}
Det en programmerer ønsker CPU-en skal utføre er følgende: 

i = 1: S = 0 + 1 = 1
i = 2: S = 1 + 2 = 3
i = 3: S = 3 + 3 = 6
og så avslutte. Om dette var et C-program, ville variablene S og i lagres i RAM og lastes inn i registrene under beregningene. Nå skal vi skrive en optimalisert maskinkode for vår maskin, hvor S og i lagres i registrene Dette gjør at beregningen går hurtigere, fordi det tar relativt lang tid å lese og skrive til RAM. Følgende er et såkalt Assembly-program som utfører denne beregningen. Assembly er et språk som ligger svært nær maskinspråk, det bruker symboler for maskininstruksjoner slik at det er lettere å lese for et menneske. Det har i motsetning til høynivåspråk en enkel en-til-en oversettelse til maskinspråk. 

0 MOVI R0 <- 3            (MOV Integer. maksverdien i for-løkken legges i R0)
1 MOVI R1 <- 1            (tallet som i økes med for hver runde i løkken)
2 MOVI R2 <- 0            (variabelen i lagres i R2)
3 MOVI R3 <- 0            (S = 0)
4 ADD R2 <- R2 + R1       (i++)  
5 ADD R3 <- R3 + R2       (S = S + i)
6 CMP R2 R0               (COMPARE, er i = 3 ? ) 
7 JNE 4                   (Jump Not Equal 4, hopp til linje 4 hvis i != 3)
Dette er slik programmet kan gjennomføres med maskin-instruksjoner og for å kunne programmer vår maskin, må nå dette programmet skrives binært med enere og nuller. Da trenger vi å vite litt av instruksjonssettet for maskinen. Vår CPU er konstruert slik at instruksjonene består av 8 bit. De fire første bit'ene definerer hvilket nummer instruksjonen er i rekken av instruksjoner. Bit nummer 5 og 6 er første operand og nr 7 og 8 er andre operand. Vanligvis bestemmer det to-bits tallet i operanden hvilket register som er involvert. Instruksjonene vi trenger til vårt program er:

binært Nr operand1 operand2 Nr Navn
0010 DR tall 2 MOVI
0100 DR SR 4 ADD
1100 DR SR 12 CMP
1111 nr nr 15 JNE


Den første linjen betyr at MOVI er instruksjon nummer 2 og at den gjør at tallet gitt ved de to siste bit'ene i instruksjonen legges i register nr DR (Destination Register). Instruksjonen ADD er nummer 4 og den legger sammen DR og SR(Source Register) og legger svaret i DR. Instruksjon nr 12 er CMP og den sammenligner DR og SR. Til slutt er instruksjon nummer 15 JNE(Jump Not Equal) som hopper til linjenummeret definert av de fire siste bit'ene i instruksjonen, hvis registrene sammenlignet i forrige instruksjon var ulike. Når vi vet dette kan vi oversette Assembly-programmet vi skrev til maskinkode som kan lastes inn i maskinens ROM:

Linje Nr I Nr DR SR
0 0010 00 11
1 0010 01 01
2 0010 10 00
3 0010 11 00
4 0100 10 01
5 0100 11 10
6 1100 10 00
7 1111 01 00


Første instruksjon er MOVI (0010) og den legger tallet 3 (11) i register nummer 0 (00, det vil si R0 Og tilsvarende for de andre instruksjonene. En kompilator oversetter direkte fra høynivåkode til tilsvarende maskinkode som kan kjøres direkte av datamaskinene. Ved å laste maskinkoden inn i Digital Works-simuleringen, kan man se hvordan dette programmet kjøres instruksjon for instruksjon og til slutt produserer resultatet S = 6.

I prinsippet fungerer moderne CPUer på samme måte som i denne simuleringen. En vesentlig forskjell er at også maskininstruksjonene hentes fra RAM. Da dette tar litt tid og da noen instruksjoner er litt mer omfattende en andre, kan det i noen tilfeller ta mer enn en klokkesyklus å få utført en instruksjon.

3.10 Løkker og branch control

Legg merke til at siste instruksjon hopper til linje 4, basert på sammenligningen av to registre i forrige instruksjon. Denne muligheten er svært viktig, for den gjør det mulig å utføre alle slags løkker, som for og while-løkker og i tilleg if-tester. I alle disse tilfellen må utførelsen kunne velge å hoppe til et annet sted i programmet basert på et resultat. JNE-instruksjonen (Jump Not Equal) gjør at man hopper til en adresse hvis sammenligningen av to registre i forrige instruksjon viste at de er forskjellige.

Hvis man ikke kunne hoppe i koden, ville man bare kunne utføre instruksjoner etterhverandre fra første til siste instruksjon og programmene måtte være enormt lange. Et program med en milliard linjer ville kunne utføres på omtrent ett sekund. Fig. 36 ser vi at det er to bit i DATAPATH, Z og co, som leder til en liten del av CPU-en som kalles branch controll. Disse styrer sammen med to bit fra instruksjonsdekoderen om programkontrollen bare skal oppe til neste instruksjon som den vanligvis gjør når program counter teller oppover, eller om PC istedet skal hoppe til det 4-bits tallet som kommer inn fra de 4 siste bit i ROM der instruksjonen inneholder adressen det eventuelt skal hoppes til.

Branch control gjør at denne enkle CPU-en kan utføre if, for og while og med det i prinsippet kan utføre alle mulige dataprogrammer. Begrensningen en firebits registerstørrelse utgjør er det lett å fjerne ved å bare øke registerstørrelsen til for eksempel 64 bit som de fleste vanlige Intel og AMD CPUer bruker. Logikken er den samme, det blir bare veldig mange flere ledinger å holde styr på.

Totalt kan denne maskinen forøvrig gjøre åtte instruksjoner(men store og load som laster inn og ut fra RAM har bugs):

binært Nr operand1 operand2 Nr Navn Funksjon
0000 DR SR 0 MOV R[DR] $\longleftarrow$ R[SR]
0010 DR tall 2 MOVI R[DR] $\longleftarrow$ tall
0100 DR SR 4 ADD R[DR] $\longleftarrow$ R[DR] + R[SR]
0110 DR SR 6 SUB R[DR] $\longleftarrow$ R[DR] - R[SR]
1000 DR SR 8 LOAD R[DR] $\longleftarrow$ M[R[SR]]
1010 DR SR 10 STORE M[R[DR]] $\longleftarrow$ R[SR]
1100 DR SR 12 CMP R[DR] - R[SR] = 0?
1111 nr nr 15 JNE PC = nr nr hvis like


Hvilke instruksjoner som kan utføres, hvordan de er nummerert, hva operandene betyr og hvordan de skal tolkes, utgjør tilsammen maskinarkitekturen. Den vanligste arkitekturen i våre dager i PCer og servere er X86-arkitekturen som ble innført av Intel i 1978 og som også brukes av AMD. Men den aller mest produserte prosessoren er basert på ARM (Advanced RISC Machine) som brukes i mobiler. Det var i 2017 produsert mer enn 100 milliarder ARM-prosessorer og 200 milliarder ble passert i 2021.


Hårek Haugerud 2025-05-07